Introduction
This project aims to infer to infer the different layers that were given as input to a neuronal model. The output of the model is then transformed into a BOLD model. Finnaly, the sbi_toolbox is used to infer the different simulation parameters.
Contributing
This project originates from the MSB1013 - Computational Neuroscience course of 2023. Find the list of contributors here.
License
The source code and documentation are realeased under the MIT License.
Simulating a multi-layered neuronal model
The mechanistic framework is based on the Dynamic Mean-Field model, a mathematical and computational framework used in neuroscience to study the dynamics of large-scale neural networks. It provides a simplified description of how the activity of neural populations can be modelled using the mean firing rate of the whole neuron population. We use the multi-layered model by Evers et al., as it adds cell-type specific connectivity to the balanced random network model developed by Van Vreeswijk et al. and Amit et al. Large-scale simulations of spiking neurons allow us to link structural information to neuronal activity. In the Dynamic Mean Field (DMF) model provided by Evers et al. 1, we first define the initial conditions of the system and the parameters, shown in Table 1 below as well as the connection probability and the structural connectivity of the local cortical layers Evers et al. shown in 1, where four out of the six layers (since 2 and 3 are combined) receive external thalamo-cortical input stimulation represented by the grey arrow. Each layer has both inhibitory (circles) and excitatory (triangles) populations of model neurons. The number of neurons in each population is extracted from 2. As for the connections, the excitatory (black) and inhibitory (grey) represent the connections between populations.
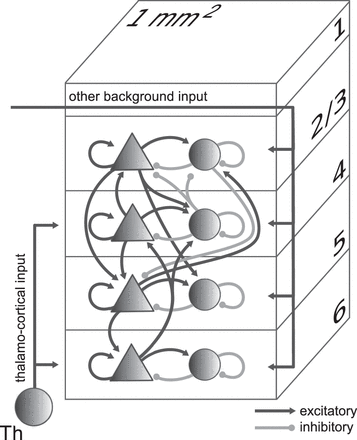
Figure 1: Model Definition. Extracted from Potjans et al. 3
Once all the general parameters have been established, we need to specify the simulation parameters. The simulation consists of three different parts. First, we have the pre-stimulation period of 0.5 seconds of no-input simulation. Then, we continuously stimulate a specific amplitude to two different neuronal populations for 2 seconds. Finally, there is the post-stimulation period, also known as the “baseline” where no external input is present. This last one extends for 10.5 seconds because the output of this simulation is later used to extract the BOLD signal, and the BOLD signal appears with a significant delay after the corresponding neuronal activity. Finally, we need to define the input current. We chose a range of stimulation input currents with intensities going from 50 to 300mA in 50mA jumps. Moreover, to the selected value from 4 the mentioned ranges, we add random uniform noise ranging from 50mA above and below that value to ensure we get the maximum uniformity in the input. These values are combined so that each simulation stimulates 2 out of the 8 populations, whether they are excitatory or inhibitory. The two intensities can also affect the same layer. So in the end we have an array with the layer combination as well as the input combination. It is important to keep the values since they are needed to train the neural net. The simulations were run in batches of 10 to reduce the computational burden. A baseline data set that included the simulation for those 10.5 seconds with no stimulus was saved. The baseline is independent of the simulation parameters because there is no current applied in this time interval. Therefore, an overall baseline array was saved and appended at the end of every simulation to optimize the code and reduce simulation time. We did all layer and input current combinations five times, for a total of 11520 simulations. As this was not enough data for the machine learning model, the process was repeated twice, for a total of 34560 simulations. The result for each simulation is the recorded intensity for each neuronal population. The appropriate function was extracted from Evers et al. 1. This variable, named Y, provides information about how the population’s activity changes in response to the experimental conditions, and it is the input for the next stage of this project.
| symbol | description | value |
|---|---|---|
| \( \sigma\) | noise amplitude | 0.02 |
| \( \tau_m \) | membrane time constant | 10e-3 |
| \( C_m \) | membrane capacitance | 250e-6 |
| \( R \) | membrane resistance | \( \frac{τ_m}{C_m} \) |
| \( g \) | inhibitory gain | -4 |
| \( M \) | number of populations | 8 |
| \( J_E \) | excitatory synaptic weight | 87.8e-3 |
| \( J_I \) | inhibitory synaptic weight | -35,12e-2 |
1: Kris S Evers, Judith Peters, and Mario Senden. “Layered Structure of Cortex Explains Reversal Dynamics in Bistable Perception”. In: bioRxiv (2023), pp. 2023–09.
2: Tom Binzegger, Rodney J Douglas, and Kevan AC Martin. “A quantitative map of the circuit of cat primary visual cortex”. In: Journal of Neuroscience 24.39 (2004), pp. 8441– 8453.
3: Tobias C Potjans and Markus Diesmann. “The cell-type specific cortical microcircuit: relating structure and activity in a full-scale spiking network model”. In: Cerebral cortex 24.3 (2014), pp. 785–806.
BOLD Coupling
The output of the neuron population simulation is then passed through a second model that combines and transforms the neuronal signal into a BOLD response. We used a modified version of the Balloon-Windkessel model, a biophysical model which considers the viscoelastic properties of blood vessels formulated by Havlicek et al. as follows [22].
- Neural Signal Pre-processing
- Neurovascular Coupling
- Haemodynamics
- BOLD response
- General Linear Model
Neural Signal Pre-processing
The BOLD signal is best correlated to changes in local-field potential (LFP) [23], which can be estimated by summing the values of the currents from the excitatory and inhibitory populations. [24] However, the model used in this project is tuned for taking inputs from a single excitatory population.[22]
For our simulations, the neural signal involved in the neurovascular coupling is the sum of the absolute values of inhibitory and excitatory populations per layer. We further 5 down-sample this current to a sampling rate of 1000 Hz, a time resolution sufficient to estimate the BOLD response. We also scale the amplitude of the signal, as the balloon model is tuned for neural activity described in terms of the proportion of activity with values between 0 and 1. Since we are mainly interested in the relative proportions of the activity in the different layers, the maximum value of all layers in one simulation is mapped to the maximal activity 1.
The baseline is removed by using the mean values during the absence of a stimulus. Furthermore, absolute values are used because only the strength of the current is relevant. We refer to this as the neural activity input for the BOLD model. The model will be applied to each layer separately and treated as independent, as the balloon model does not account for (cortical) depth.
Neurovascular Coupling
Some of the neural signal information is lost in the neurovascular coupling, thus acting like a lowpass filter. This filtered signal can be interpreted as the vasoactive signal, which then influences the blood inflow level. The inflow of blood then affects the stretch of the blood vessels, imposing feedback on the vasoactive signal and having the neurovascular coupling behaviour reflect the properties of a damped oscillator. 1
\[\dot{s} = X(t) − ϕ · s(t) \]
where:
- \(s\) = vasoactive signal
- \(X\) = neural signal (units)
- \(ϕ\) = rate constant (controlling response decay)
\[f˙ = Φ · s(t) − χ · f_{in}(t) \] where:
- \(f_in\) = inflow of blood into the model (units?)
- \(Φ, χ\) = rate constant (controlling response decay)
1: Martin Havlicek et al. “Physiologically informed dynamic causal modeling of fMRI data”. In: NeuroImage 122 (Nov. 2015), pp. 355–372. issn: 1053-8119. doi: 10 . 1016 / J . NEUROIMAGE.2015.07.078.
Haemodynamics
The following equations represent mass balance equations for blood volume and deoxyhaemoglobin into the cortical column as the venous compartment expands (like a balloon). These equations describe the physiological aspect of large amounts of blood inflow increasing locally to support small increases in oxygen metabolism rates and an associated change in oxygen extraction fraction. 1
\[\dot{V}=\frac{f_{in}(t) − f_{out}(t)}{\tau} \]
\[\dot{q} =\frac{ f_{in}(t)\frac{E_f}{E_0} − f_{out}(t)\frac{q(t)}{V(t)} }{τ} \]
where:
\[ \dot{E_{f}} = 1 − \frac{1 − E_0}{1 − f_{in}(t)} \]
\[ \dot{f_{out}} = V (t) \frac{1}{\alpha} + \tau_{vs} \]
- \(V \) = blood volume (normalized with respect to resting state value)
- \(Q \) = deoxyhemoglobin levels (normalized with respect to resting state value)
- \(f_{out}\) = outflow of blood from the model
- \(\tau \) = time constant
- \(E_f\) = oxygen extraction fraction
- \(E_0\) = baseline oxygen extraction fraction
- \(τ_{vs}\) = viscoelastic time constant
1: Martin Havlicek et al. “Physiologically informed dynamic causal modeling of fMRI data”. In: NeuroImage 122 (Nov. 2015), pp. 355–372. issn: 1053-8119. doi: 10 . 1016 / J . NEUROIMAGE.2015.07.078.
BOLD response
Finally, all of the previous equations are combined into a final formula that describes the rate of change on the BOLD signal, depending on the relative amount of deoxyhaemoglobin and blood volume in the cortical layer. This final step is evidently dependent also on the strength of the magnetic field applied. The used parameters are shown in table 2.
\[ \dot{BOLD} = V0 · (k_1(1 − q(t)) + k_2(1 − \frac{q(t)}{V (t)} ) + k_3(1 − V (t))) \]
\(k_1, k_2, k_3 \) are magnetic field strength-dependent parameters, where:
\[k_1 = 4.3 · ν_0 · E_0 · T_E\] \[k_2 = ϵ · ρ_0 · E_0 · T_E\] \[k_3 = 1 − ε\]
where:
- \(ν_0\) = field-dependent frequency offset at the surface of a blood vessel
- \(T_E\) = MRI echo time
- \(ε\) = ratio of intra to extravascular fMRI signal contribution
- \(ρ_0\) = sensitivity of vascular signal relaxation rate with regards to changes in oxygen saturation
However, LBR is observable only in ultra-high field MRI (7+ Tesla), where ε becomes negligible [22]. Therefore, we use:
\[k_1 = 4.3 · ν_0 · E_0 · T_E \] \[k_2 = 0 \] \[k_3 = 1 \]
The BOLD response these equations provide does not start at zero but requires some time to settle into its baseline. To account for this, all values before the beginning of the stimulus are set to the value of the BOLD response at the start of the stimulus start. This way, it is ensured that the BOLD signal does not deflect the stimulus yet but has time to settle into its baseline.
| Symbol | Description | Value |
|---|---|---|
| ϕ | rate constant | 0.6 |
| Φ | rate constant | 1.5 |
| χ | rate constant | 0.6 |
| E0 | baseline oxygen ejection fraction | 0.4 |
| τ | time constant | 2 |
| α | Grubb’s exponent | 0.32 |
| τvs | viscoelastic time constant | 4 |
| V0 | baseline blood volume | 4 |
| ν0 | frequency offset at the blood vessel surface | 188.1 |
| TE | echo time | 0.028 |
| ε | ration of fMRI signal contribution | 0 |
| r0 | sensitivity | - |
Table 2: Parameter Values Used in the BOLD Model.
General Linear Model
The General Linear Model (GLM) is widely used in fMRI analysis, combining knowledge about the experimental design, i.e. the timing of the stimulus and the BOLD morphology. The general idea is to find parameters linking the obtained BOLD responses to an idealized BOLD response, describing the contribution of each of the layers. Because the BOLD signal is known to follow a consistent shape, it can be modelled using the hemodynamic response function (HRF) [25]. This is used as our design matrix. By combining it via convolution with our condition array indicating the time interval of the stimulus and normalising the result between 0 and 1, we obtain an idealized BOLD response for each layer.
GLM is then used to obtain a set of parameters \(β\)s that describe the relation between the simulation of the BOLD response Y given the neural active and the created model X, which only contains information about the timing of the stimulus. Therefore, each coefficient \(β\) quantifies the amount of activity seen in each layer. In this project’s scope, each layer is considered a voxel.
The GLM is expressed as
\[Y = Xβ + e.\]
with \(Y ∈ ℝ^{T×4}\) of the simulated BOLD responses, \(X ∈ ℝ^{T×4}\) of the model, the parameters \(β ∈ ℝ^{4×4}\) and \(e ∈ ℝ^{T×N}\) being the residual term. This is mathematically identical to multiple regression analysis and can be solved using Least Squares to find the solution with the minimized sum of squared error terms [26]: \[ \hat{β} = (X′X)^{−1}X′y \] Thus, we end with parameters describing the amplitude of each voxel’s fMRI. To mirror a realistic fMRI sample rate, the BOLD signal and the idealized fMRI are both down-sampled to 0.5 Hz before solving the GLM.
Neural Net Inference
A neural network was used to relate the summary statistics contained in the beta values (output of the previous GLM model) to the input injected into the various neuronal populations in the four cortical layers. The simulation-based inference (SBI) toolbox, a PyTorch package, was used for this purpose. We adapted the code available in the following GitHub repository from Kris Evers.
In short, an "X matrix" in the form of a 2D NumPy array is created containing the original 8 input currents parameters and their 4 corresponding beta values. Every array corresponds to one simulation. In total, 34560 simulations were performed, implying that the size of X is 34560 x 12. As the generation of the data matrix was done in a linear manner, to ensure that the test data had an even distribution of combinations, the matrix was randomly shuffled and split into a train and test set where 10% (3456 simulations) are assigned as test data.
In the process of training the neural network, the neural network has an initial density estimator attached to the model. The training set was further divided into the parameters and beta values by separating the last 4 columns containing the beta values from the first eight columns that contain the parameters. Then, the model can be trained using the Sequential Neural Posterior Estimation (SNPE) algorithm. Simulation data is appended to the model in order to establish training data for the model. [27]. This was done with the help of a Masked Autoregressive Flow (MAF) neural density estimator.
After training the model, this model was saved as an intermediary result to avoid the need to retrain the network for future implementations. It is worth noting that in the SBI toolbox, 2 other algorithms are given, namely SNLE (for likelihood estimation) and SNRE (for likelihood-ratio estimation). However, these two methods require a prior distribution to be defined prior to training. Due to the nature of the simulation data, this approach was not pursued. The process of shuffling, splitting and training the model was performed 10 times to avoid the scenario where a bad training and/or test set is acquired by chance. That is, 10 different posterior models were trained (posterior_n, where n = 1 to 10) with their corresponding training and test set, numbered from 1 to 10.
Training
Testing
To test the generated posterior models, a testing method was established to evaluate statistics based on a testing matrix. This testing matrix is split similarly to the training data, where 9 the beta values and parameters are separated into the observation and the target parameters. The aim of the testing was two-fold: To assess whether it could infer which populations were active given the summary statistics generated via the BOLD model and whether the model could actually predict the level of activation given to a specific population. The hypothesis was that the model was more likely to predict whether a population was active or not rather than being able to establish the level of activation. When testing a prediction, the posterior is given an observation via set_default_x(), and then sampled according to the testing parameter num_sample. This produces an array of predictions for a given observation. To establish the prediction of the activity of a given population, the value of the 50th percentile is calculated. A prediction array can then be built on the value predicted for each population. To assess the quality of the inference, multiple metrics were created.
Metrics
Test specific metrics
- The first metric was a binary prediction of whether a layer is predicted to be active or not. The testing parameter activation_threshold establishes at what value a population input value should be to be considered active. A binary prediction array is then built to highlight the populations the prediction deemed active. This is done on the true values and then compared to establish if the prediction was able to infer which populations were correctly active.
- The second metric is the percentage of samples that give a value that lies in a confidence range. As such, two parameters were established: threshold and tolerance. The threshold is a percentage of the true value and the tolerance is an absolute value. The range is then given as: \[ truevalue(1 − threshold) − tolerance ≤ predictedvalue ≤ truevalue(1 + threshold) + tolerance \]
An array is then constructed to keep track of the range of values predicted by the sampling. This allows for a simpler interpretation of the shape of the distribution. Indeed, it can be understood as the confidence of the prediction in the actual value.
Model specific metrics
To evaluate the performance of the model on a particular testing data set, the balanced accuracy was calculated. This was first done on each population, and then on combinations of activation. The rationale behind this was that a prediction might be able to detect one population but not the other one in the case where two populations were activated. As such, a confusion matrix alongside the balanced accuracy using the binary prediction array was computed per population. Furthermore, the choice of balanced accuracy was motivated by the fact that the data set was heavily unbalanced where for a given population it was inactivated around 80% of the time. The balanced accuracy was calculated as follows: \[\text{Balanced}_\text{accuracy} = \frac{1}{2}(\frac{TP}{TP + FP}+\frac{TN}{TN + FN}) \]
where \(TP\) = True positives, \(FP\) = False positives, \(TN\) = True negatives and \(FN\) = False negatives A confusion matrix was also calculated for each combination of populations to investigate the prediction accuracy further. That is, given a prediction, was the model able to predict the activation state of two layers accurately?
Data set specific metrics
Finally, the overall accuracy was evaluated per model by averaging the balanced accuracy evaluated per population.
Generating Data
Contributors
Here is the list of the contributors to this project who helped in developing this project. Thanks yall
Students
- Zianor
- CheYeeNg
- apantebre
- Sofixon
- Sonia
- Rodrigo
Advisors
- Mario
- Kris